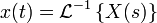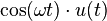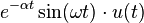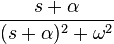Automatismo y Control Jon: mayo 2012

3ª PRÁCTICA

En esta práctica trabajaremos de nuevo con Matlab de dos formas:

- Haciendo uso de Simulink para elaborar diagramas de bloques y ver mediante una gráfica sus respuestas temporales.

- Usando la transformada de LaPlace.

1ª Parte: Sistema de primer orden

En primer lugar empezaremos haciendo un ejercicio con diagramas de bloques, haciendo uso de las herramientas de Simulink.

Para abrir la pantala donde pondremos los bloques tenemos que ir a File-New-Model y se nos abrirá una ventana en blanco donde iremos insertando los elementos de Simulink.

Primero tenemos que crear e bloque de función de transferencia que se ve en la figura (el que está en medio).Para ello vamos a la barra de herramientas donde pone Simulink y luego en Continuous/Transfer Fcn y arrastramos a la página en blanco.

Para introducirle la función que le queramos poner (dependerá de ejercicio) hacemos doble click en Transfer Fcn y ponemos entre corchetes los coeficientes del polinomio del numerador y denominador.

- Numerator coefficients [A]

- Denominator coeffiicients [1+a]
- Luego le damos a OK

En nuestro caso: G=A/(s+a) donde A=10 y a=2

Ahora tenemos que crear delante de función de transferencia un bloque que contenga la función "step".

Para ello vamos a Simulink pinchamos en Sources y arrastramos a la pantalla (la del model) el icono de "Step"

A continuación creamos detrás del bloque de Transfer Fcn un bloque que ponga "Scope" para ello hacemos el mismo procedimiento que para "step" pero pinchando en Sinks.

Hacemos doble click en el bloque "step" y ponemos los parámetros, que en nuestro caso son:

step time=0
initial value=0
final value=5
step time=0

Unimos con flechas los 3 bloques.
Lo que se ve en el scope el la respuesta temporal de primer orden para la entrada step (escalón)

Para acabar:
- simulation
- start

Así obtenemos la gráfica:

2ª Parte: Sistemas de 2º orden

Esta segunda parte es similar a la primera pero con una ecuación de 2º grado.

Consta de dos ejemplos uno sencillo y otro más complejo:

1º EJERCICIO

Utilizaremos los mismos bloques,pero cambiaremos el numerador y el denominador del bloque de función de transferencia por:

A*(wn)^2/(s^2+2*wn*xi*wn^2) siendo: A = 2 un valor

wn=7 pulsación natural

xi = 0.2 coeficiente de amortiguamiento

Al igual que en la 1ª parte introducimos los coeficientes:

[A*wn^2]/[1 2*wn*xi wn^2]

Obtenemos la gráfica siquiente:

2º EJERCICIO (más complejo)

Es similar al anterior pero ahora introduciremos un nuevo elemento (gain).

Para insertar el bloque "gain" tenemos que ir a Commonly Used BI y escogemos gain

En este caso el bloque de función de transferencia contiene la función:
1/(a*s^2+bs) Donde a=2 b=3

y el bloque gain: c Donde c = 5

NOTA: Para girar el triángulo:
-Le damos un click en el triángulo
-Icono Format
-Dar a Flip Block

3ª Parte: Respuesta temporal a partir de la Transformada de LaPlace

Sistema de primer orden:

G=A/(s+a)

U=1/s (transformada de LaPlace de la función step)

U-->G-->Y

Y(s)=G(s)*U=A/(s*(s+a))

y(t)=L^-1[Y(s)] (Tranformada inversa de LaPlace de Y(s))

Matlab

A=10 ; a=2
syms t s
Y=A/((s+a)*s)
y=ilaplace(Y,s,t)
ezplot(y,[0,5]),axis([0,5,0,7]) siendo 0 la x min y 5 la x max
siendo 0 la y min y 7 la y max

Sistema de 2º Orden:

Matlab

A=2
wn=7
xi=0,2
syms t s
Y=A*wn^2/(s*(s^2+2*xi*wn*s+wn^2))
y=ilaplace(Y,s,t)
ezplot(y,[0,5]),axis([0,5,0,7])

2ª PRÁCTICA: MATLAB

¿Qué es Matlab?

MATLAB (abreviatura de MATrix LABoratory, "laboratorio de matrices") es un software matemático que ofrece un entorno de desarrollo integrado (IDE) con un lenguaje de programación propio (lenguaje M). Está disponible para las plataformas Unix, Windows y Apple Mac OS X.

Entre sus prestaciones básicas se hallan: la manipulación de matrices, la representación de datos y funciones, la implementación de algoritmos, la creación de interfaces de usuario (GUI) y la comunicación con programas en otros lenguajes y con otros dispositivos hardware.

El paquete MATLAB dispone de dos herramientas adicionales que expanden sus prestaciones, a saber, Simulink (plataforma de simulación multidominio) y GUIDE (editor de interfaces de usuario - GUI). Además, se pueden ampliar las capacidades de MATLAB con las cajas de herramientas (toolboxes); y las de Simulink con los paquetes de bloques (blocksets).

Es un software muy usado en universidades y centros de investigación y desarrollo. En los últimos años ha aumentado el número de prestaciones, como la de programar directamente procesadores digitales de señal o crear código VHDL.

1º Parte: Operaciones con números reales

En esta parte haremos operaciones con números reales.Para ello se utilizan los operadores básicos: suma, resta, división y multiplicación +, -, /, *

Ejemplo de operación aritmética:

2ª Parte: Operaciones con números complejos

Los números complejos se pueden denominar de dos formas diferentes:

- Forma binómica: z=a+bi
- Forma polar: z=(r,α) donde r es el módulo de z y α es un argumento de z.

Se el módulo mediante la expresión: abs(z)
Se obtiene el argumento mediante la expresión: angle(z)

3ª Parte: Operaciones con matrices

Si queremos introducir un a matriz A:

>> A = [1 2 3;4 5 6;7 8 0]

Si queremos hacer la matriz traspuesta: x=[4 3 -7]'

Si queremos generar una matriz aleatoria: B=rand(3,3)

Si queremos calcular el rango de una matriz: rank(B)

Para hallar el determinante de una matriz introducimos: det(A)

MATRICES

OPERACIONES CON MATRICES

4ª Parte: Cálculo simbólico

Para calcular derivadas usaremos el comando: r=diff(p,x)
siendo p la expresión que vamos a derivar y la x indica la variable respecto a la cual derivaremos.

Para calcular integrales indefinidas: u=int(p,x)
siendo p la expresión que vamos a integrar y la x significa respecto a que variable debemos integrar .

Para calcular integrales definidas: u=int(p,x,a,b)
siendo p y la x significan lo mismo que en la integral indefinida anterior y la a y b son los límites de integración.

Para introducir raíces cuadradas ponemos sqrt()

DERIVADAS

INTEGRALES

POLINOMIOS

5ª Parte: Gráficos

Para dibujar gráficas tenemos que introducir el intervalo de valores que queramos por ejemplo:

x=[-2:0.1:2] En este caso la gráfica la dibujara desde -2 hasta 2 calculando los valores de y cada 0,1
y=x.^2

Finalmente para que dibuje la gráfica escribimos: plot(x,y)

En la práctica hicimos tres ejercicios que son los siguientes:

y=x^2

y=sin(x)

y=sin(x) (help plot)

6ª Parte: m files

Puedo escribir lo que escribo en matlab en el editor de texto y guardarlo en .m. El matlab tiene un editor que se abre en File/New/Script

Cuando ya tenemos el código escrito en el editor podemos ejecutarlo directamente desde Matlab poniendo por ejemplo, si un archivo se llama ej1.m

Pra ello introducimos:

>>ej1 y luego ENTER

1ª PRÁCTICA - Java con jEdit

jEdit es un editor de texto libre, distribuido bajo los términos de la Licencia pública general de GNU. Está escrito en Java y se ejecuta en Windows, GNU/Linux, Mac OS X y otros sistemas operativos que dispongan de la máquina virtual Java.

La práctica consiste en la realización de tres ejercicios:

1-Hello World.
2-Suma de dos números.
3-Applet para poder trazar una línea recta entre dos puntos.

Los pasos para a seguir son:

1º Insertamos el código

2º Guardamos el programa con el mismo nombre y la extensión .java. Si no se realiza este paso correctamente el programa dará error.

3º Compilamos el programa: Plugins > Console > Compile Current Buffer.

4º Ejecutamos el programa: Plugins > Console > Run Current Buffer.

1º Hello World

Escribimos el siguiente código:

class HelloWorld {
public static void main(String[] args)
{
System.out.println("Hello World!");
}
}

2º Sumar Numeros

Código:

//----JAVA SUMA DE DOS VARIABLES.
import javax.swing.JOptionPane;

public class SumarNumeros {

   public static void main( String args[] )
   {
      String strNumero1;
      String strNumero2;
      int intNumero1;
      int intNumero2;
      int suma;
      strNumero1 = JOptionPane.showInputDialog( "Ingrese el entero 1" );
      strNumero2 = JOptionPane.showInputDialog( "Ingrese el entero 2" );
      intNumero1 = Integer.parseInt( strNumero1 );
      intNumero2 = Integer.parseInt( strNumero2 );

      suma = intNumero1 + intNumero2;

      JOptionPane.showMessageDialog(
         null, "La suma es " + suma, "Resultado,",
         JOptionPane.PLAIN_MESSAGE );
     System.exit( 0 );
}
}

3º Simple Line (Applets)

Creamos un archivo llamado SimpleLine.java

Código:

Archivo Java:

import java.applet.*;

import java.awt.*;

public class SimpleLine extends applet {

public void paint ( Gaphics g ) {

g.drawLine ( O, O, this.getSize().width, this.getSize().height);

}

Archivo html:

<html>

<head> <title> hello world </title> </head>

<body>

This is the applet:<P>

</applet>

</body>

</html>

Ecuaciones Diferenciales Ordinarias (EDO)

Una ecuación diferencial ordinaria (comúnmente abreviada "EDO") es una relación que contiene funciones de una sola variable independiente, y una o más de sus derivadas con respecto a esa variable.

Las ecuaciones diferenciales ordinarias son importantes en diversas áreas de estudio como la geometría, mecánica y astronomía, además de muchas otras aplicaciones.

Tipos

Existen diversos tipos de ecuaciones diferenciales ordinarias, cada una con una forma de resolución distinta; para clasificarlas, hay que hacer la diferencia entre ecuaciones diferenciales de primer orden y ecuaciones de orden superior (ya que las primeras son, por lo general, de más fácil resolución).

Transformada de Laplace

La transformada de Laplace de una función f(t) definida (en ecuaciones diferenciales, o en análisis matemático o en análisis funcional) para todos los números positivos t ≥ 0, es la función F(s), definida por:

$F(s) = \mathcal{L} \left\{f(t)\right\} =\int_{0}^\infty e^{-st} f(t)\,dt.$

siempre y cuando la integral esté definida.
Sirve para facilitar el cálculo de las ecuaciones diferenciales.

Forma integral

Una fórmula integral para la transformada inversa de Laplace, llamada fórmula inversa de Mellin, es dada por la integral lineal:

$\mathcal{L}^{-1}\{F(s)\} = f(t)= \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty}e^{st}F(s)\,ds,$

Propiedades

Linealidad

$\mathcal{L}\left\{a f(t) + b g(t) \right\} = a \mathcal{L}\left\{ f(t) \right\} + b \mathcal{L}\left\{ g(t) \right\}$

Tabla de las transformadas de Laplace mas importantes:

ID	Función	Dominio en el tiempo $x(t) = \mathcal{L}^{-1} \left\{ X(s) \right\}$	Dominio en la frecuencia $X(s) = \mathcal{L}\left\{ x(t) \right\}$	Región de la convergencia para sistemas causales

1a	impulso unitario	$\delta(t) \$	$1 \$	$\mathrm{todo} \ s \,$

2a.2	escalón unitario	$u(t) \$	${ 1 \over s }$	$s > 0 \,$

2d.1	amortiguación exponencial	$e^{-\alpha t} \cdot u(t) \$	${ 1 \over s+\alpha }$	$s > - \alpha \$

4	seno	$\sin(\omega t) \cdot u(t) \$	${ \omega \over s^2 + \omega^2 }$	$s > 0 \$
5	coseno	$\cos(\omega t) \cdot u(t) \$	${ s \over s^2 + \omega^2 }$	$s > 0 \$

8	onda senoidal con amortiguamiento exponencial	$e^{-\alpha t} \sin(\omega t) \cdot u(t) \$	${ \omega \over (s+\alpha )^2 + \omega^2 }$	$s > -\alpha \$
9	onda cosenoidal con amortiguamiento exponencial	$e^{-\alpha t} \cos(\omega t) \cdot u(t) \$	${ s+\alpha \over (s+\alpha )^2 + \omega^2 }$	$s > -\alpha \$