Automatismo y Control Jon: Transformada de Laplace

La transformada de Laplace de una función f(t) definida (en ecuaciones diferenciales, o en análisis matemático o en análisis funcional) para todos los números positivos t ≥ 0, es la función F(s), definida por:

$F(s) = \mathcal{L} \left\{f(t)\right\} =\int_{0}^\infty e^{-st} f(t)\,dt.$

siempre y cuando la integral esté definida.
Sirve para facilitar el cálculo de las ecuaciones diferenciales.

Forma integral

Una fórmula integral para la transformada inversa de Laplace, llamada fórmula inversa de Mellin, es dada por la integral lineal:

$\mathcal{L}^{-1}\{F(s)\} = f(t)= \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty}e^{st}F(s)\,ds,$

Propiedades

Linealidad

$\mathcal{L}\left\{a f(t) + b g(t) \right\} = a \mathcal{L}\left\{ f(t) \right\} + b \mathcal{L}\left\{ g(t) \right\}$

Tabla de las transformadas de Laplace mas importantes:

ID	Función	Dominio en el tiempo 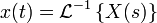$x(t) = \mathcal{L}^{-1} \left\{ X(s) \right\}$	Dominio en la frecuencia $X(s) = \mathcal{L}\left\{ x(t) \right\}$	Región de la convergencia para sistemas causales

1a	impulso unitario	$\delta(t) \$	$1 \$	$\mathrm{todo} \ s \,$

2a.2	escalón unitario	$u(t) \$	${ 1 \over s }$	$s > 0 \,$

2d.1	amortiguación exponencial	$e^{-\alpha t} \cdot u(t) \$	${ 1 \over s+\alpha }$	$s > - \alpha \$

4	seno	$\sin(\omega t) \cdot u(t) \$	${ \omega \over s^2 + \omega^2 }$	$s > 0 \$
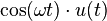
5	coseno	$\cos(\omega t) \cdot u(t) \$	${ s \over s^2 + \omega^2 }$	$s > 0 \$

8	onda senoidal con amortiguamiento exponencial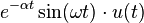	$e^{-\alpha t} \sin(\omega t) \cdot u(t) \$	${ \omega \over (s+\alpha )^2 + \omega^2 }$	$s > -\alpha \$
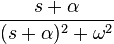
9	onda cosenoidal con amortiguamiento exponencial	$e^{-\alpha t} \cos(\omega t) \cdot u(t) \$	${ s+\alpha \over (s+\alpha )^2 + \omega^2 }$	$s > -\alpha \$

Automatismo y Control Jon

Transformada de Laplace

Linealidad

Tabla de las transformadas de Laplace mas importantes:

No hay comentarios:

Publicar un comentario

Datos personales